Many existing and evolving constraint logic programming projects resemble some ancient invention of gunpowder. For example SWI-Prologs 9.3.35 corouting for delayed goals is mainly based on unify hooks. We show how verify hooks, already used in formerly Jekejeke Prolog, can be braught to Dogelog Player in a 100% Prolog fashion.

The experimental library(edge/railgun) makes use of cyclic terms to model delayed goals. One may ask how on earth cyclic terms aka rational trees enter the picture? We observation the delay of a goal G(X) on a variable X, creates a circular dependency, if we model attributed variables as carrying the future value and the delayed goal:

:- ensure_loaded(library(edge/railgun)).

?- freeze(X, (deref(X,Y), write(Y), nl)), bind(X, hello).

In the above we see the cyclic dependency along the attributed variable modelled by a compound '$ATTR'/2. To access and modify such attributed variables we have introduced the utility predicates deref/2 and bind/2 which are usually not needed in a constraint logic programming implementation. On the other hand we see a familiar freeze/2.

?- dif(X,Y), indomain(X, [1,2,3]), indomain(Y, [1,2,3]),
   deref(X,A), deref(Y,B).

Rational trees were introduced by Alain Colmerauer in early 80's with Prolog II. In the above we see the famous dif/2 predicate, which was also already introduced by Alain Colmerauer at the same time. Our implentation is a stripped down version for atomic values that is closer to (#\=)/2 together with a backtracking binder indomain/2.

It should be noted that we do not implement the full constraint logic programming schema. For example the bind/2 predicate is not able to alias variables. Corresponding extensions are possible up to the provision of a unify/2 predicate, which can then be useful for automated theorem proving, whereas we aim more at combinatorial search.

Constraint solving utilities can be separated into predicates to setup a constraint model and into predicates to solve a constraint model. In both cases the constraint model is the same emergent structure of attributed variables, which does not only define the constraint store of delayed goals, but also the wakeup dependencies.

Among constraint solving utilities we find in our new library(edge/railgun) for example the predicate all_different/1 which allows to establish a constraint of differing variables, and the predicate label/2 which backtracks over a set of variables. In as far the constraint solving is quite open ended, people regularly invent and study new such predicates:

/* The predicate delays that all elements of L are different. */
all_different([]).
all_different([X|L]) :-
   maplist(dif(X), L),
   all_different(L).

/* The predicate binds the elements of L, left to right. */
label([], _).
label([X|L], D) :-
   indomain(X, D),
   label(L, D).

To demonstrate both predicates we generate permutations:

test(X) :-
   length(L, 3),
   all_different(L),
   label(L, [1,2,3]),
   maplist(deref, L, X).

?- test(X).

A popular problem for constraint solving is map coloring. The coloring appartness between bordering regions is easily represented by a dif/2 constraint. That four colors are enough for a planar problem, was suggested by Francis Guthrie, while trying to color the map of counties of England:

:- ensure_loaded(library(misc/aggregate)).

plane(L) :-
   L = [A,B,C,D,E,F],
   dif(A, B), dif(A, C), dif(A, D), dif(A, E),
   dif(B, C), dif(B, D), dif(B, F),
   dif(C, D),
   dif(D, E), dif(D, F),
   dif(E, F),
   label(L, [1,2,3,4]).

?- aggregate_all(count, plane(_), C).

We can use exhaustive permutation of [1,2,3,4,5,6,7,8,9] for a first benchmarking of our new library(edge/railgun) against other contstraint solving systems, that usually also provide all_different/1 and label/2. We include in our testing the 10000x times iterating the map coloring and the Trealla Prolog 2.86.3 system. We leave both Prolog systems behind:

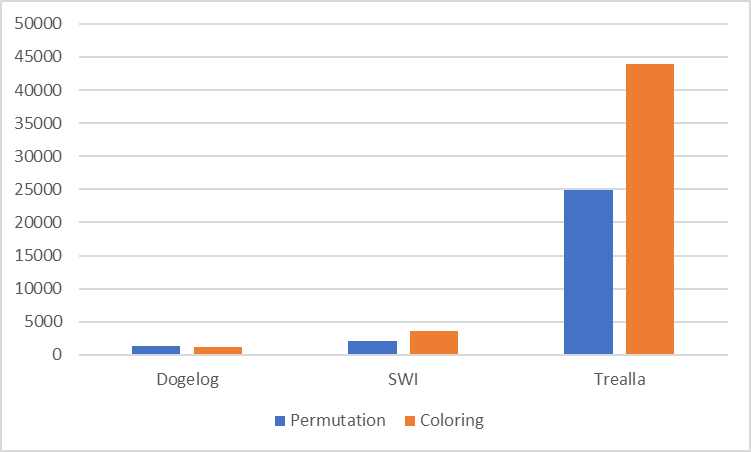
It should be mentioned that Dogelog Players 2.1.4 performance is mainly due to the use of a special built-in '$SEQ'/2, already introduced in version 0.9.0 of Dogelog Player, that allows to put a list of goals on the continuation in one shot. This is ideal for backtracking problems. But the library could be also implemented with call/1 and thus ISO core standard Prolog only.

t.b.d.